Probability & Statistics in Engineering

Fall 2023 - 14 Nov

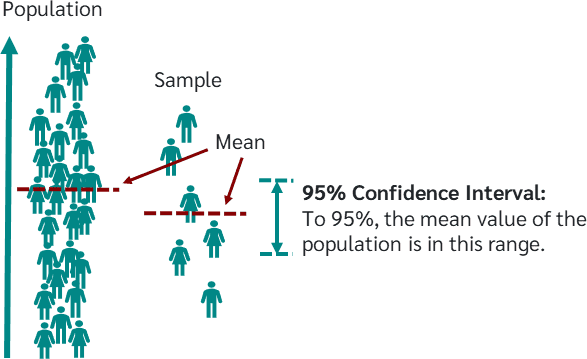
Interval estimates

  • Suppose that \(X_1\), \(X_2\),…, \(X_n\) is a sample of a normal population that has mean \(\mu\) and \(\sigma^2\)
  • The MLE estimate of \(\mu\) is \(\overline{X}=\sum_{i=1}^n X_i / n\)
  • We don't expect \(\overline{X}\) to be exactly equal to \(\mu\)
  • But it should be close
  • Rather than a point estimate we can specify an interval
  • We can assign a degree of confidence that \(\mu\) lies within that interval
  • The distribution of the point estimator can be used to obtain the interval estimator

Confidence intervals

  • An interval estimate for a population parameter
  • Usually they are 90%, 95% and 99%
  • Measure of reliability: if we repeated the experiment multiple times and calculated the 95% bounds then 95% of samples would contain the true mean within their corresponding bounds
  • Confidence interval for mean, variance and proportion
  • Cases of normal distribution with known or unknown variance

The 95% confidence interval on the mean

confidence_interval.png
https://datatab.net/tutorial/confidence-interval

Remember that \(\dfrac{\overline{X}-\mu}{\sigma / \sqrt{n}}\) is a standard normal variable

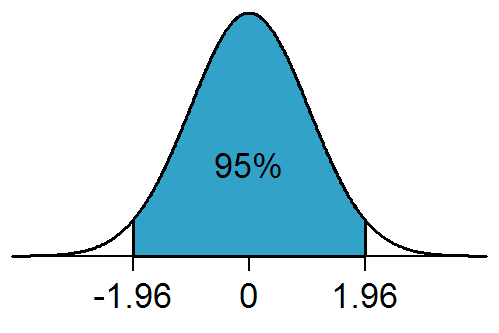
confidence_1_96.webp

\[P \left( -1.96 < \dfrac{\overline{X}-\mu}{\sigma / \sqrt{n}} < 1.96 \right) = 0.95\]

\[P \left( -1.96 \dfrac{\sigma}{\sqrt{n}} < \overline{X}-\mu < 1.96 \dfrac{\sigma}{\sqrt{n}} \right) = 0.95\]

\[P \left( -1.96 \dfrac{\sigma}{\sqrt{n}} < \mu - \overline{X} < 1.96 \dfrac{\sigma}{\sqrt{n}} \right) = 0.95\]

\[P \left( \overline{X} - 1.96 \dfrac{\sigma}{\sqrt{n}} < \mu < \overline{X} + 1.96 \dfrac{\sigma}{\sqrt{n}} \right) = 0.95\]

With 95% confidence, the true mean lies within \(1.96 \dfrac{\sigma}{\sqrt{n}}\) of the sample mean and the 95 percent confidence interval is \[\left(\overline{X} - 1.96 \dfrac{\sigma}{\sqrt{n}}, \overline{X} + 1.96 \dfrac{\sigma}{\sqrt{n}} \right)\]

Problem 17.1

The amplitude of a signal received is random variable due to noise during transmission, but it follows a distribution \(\text{N}(\mu, 4)\). If the amplitudes measured 9 times are 5, 8.5, 12, 15, 7, 9, 7.5, 6.5, 10.5 what is the 95% confidence interval for the true amplitude \(\mu\)?

Two-sided and one-sided intervals

What if we were interested in \(\mu\) being at least as large as value (relative to the mean)?

\[P(Z < 1.645) = 0.95 \Rightarrow P \left( \dfrac{\overline{X}-\mu}{\sigma / \sqrt{n}} < 1.645 \right) = 0.95\]

\[P \left( \overline{X} - 1.645 \dfrac{\sigma}{\sqrt{n}} < \mu \right) = 0.95\]

One-sided upper 95% confidence interval \[\left( \overline{X} - 1.645 \dfrac{\sigma}{\sqrt{n}}, \infty \right)\] One-sided lower 95% confidence interval \[\left(-\infty, \overline{X} + 1.645 \dfrac{\sigma}{\sqrt{n}} \right)\]

Problem 17.2

Find the upper and lower 95% confidence intervals from the previous example.

Confidence intervals of any specified level

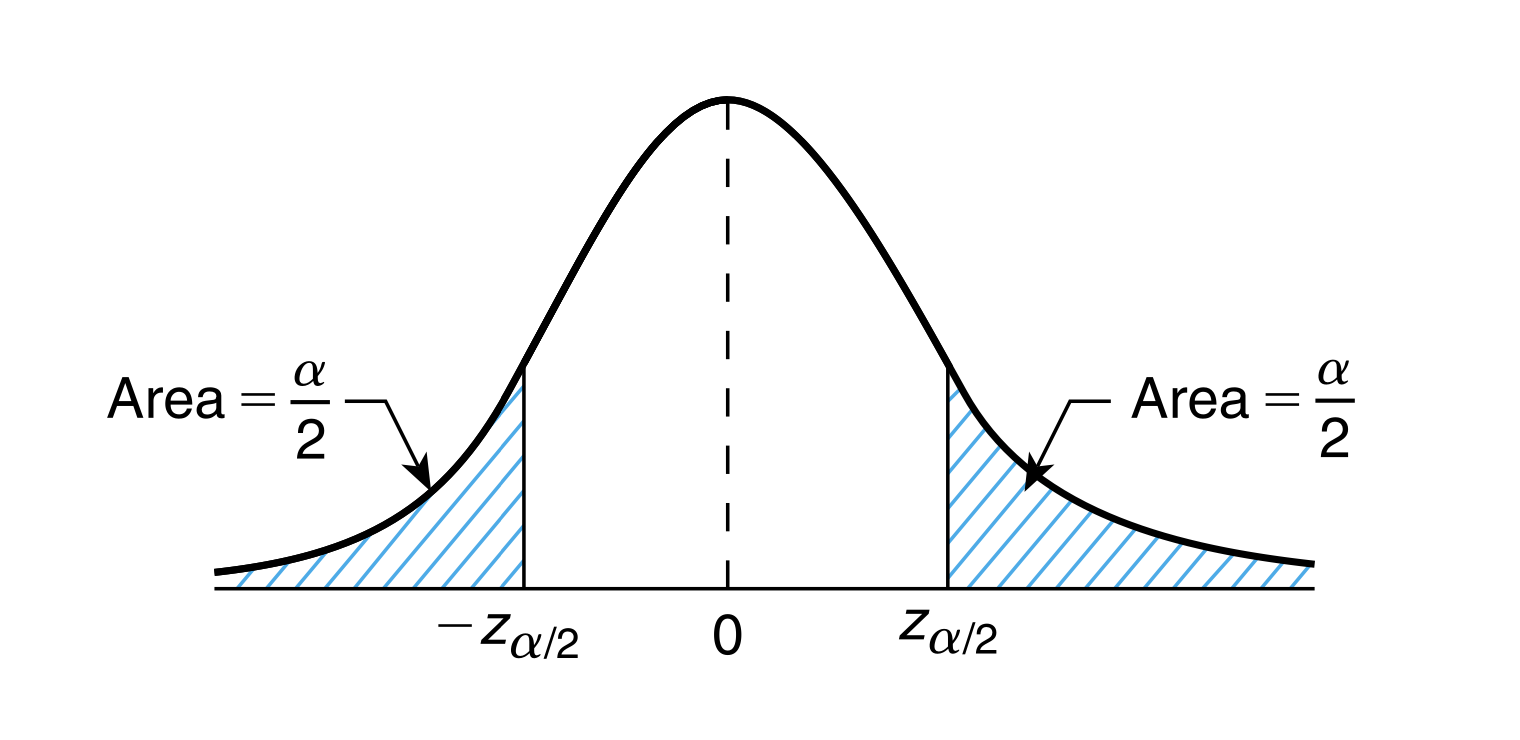
confidence_a.png

\[P(Z > z_a) = a\]

\[P \left( -z_{a/2} < Z < z_{a/2} \right) = 1-a \Rightarrow P \left( -z_{a/2} < \dfrac{\overline{X}-\mu}{\sigma / \sqrt{n}} < z_{a/2} \right)\]

\[P \left( \overline{X} - z_{a/2} \dfrac{\sigma}{\sqrt{n}} < \mu < \overline{X} + z_{a/2} \dfrac{\sigma}{\sqrt{n}} \right)\]

The \(100(1-a)\) percent two-sided confidence interval for \(\mu\) is \[\left( \overline{X} - z_{a/2} \dfrac{\sigma}{\sqrt{n}}, \overline{X} + z_{a/2} \dfrac{\sigma}{\sqrt{n}} \right)\]

The \(100(1-a)\) percent one-sided lower confidence interval for \(\mu\) is \[\left( -\infty, \overline{X} + z_{a} \dfrac{\sigma}{\sqrt{n}} \right)\] The \(100(1-a)\) percent one-sided upper confidence interval for \(\mu\) is \[\left( \overline{X} - z_{a} \dfrac{\sigma}{\sqrt{n}}, \infty \right)\]

Problem 17.3

Use the previous data to calculate the 99% confidence intervals (both two- and one-sided).

Choosing the sample size

  • Ten measurements of impact energy on specimens of steel materials had a mean of 64.46 J
  • Impact energy is normally distributed with \(\sigma=1\) J
  • How many steel material specimens do we need to keep the 99% bounds at most 1.0 J?
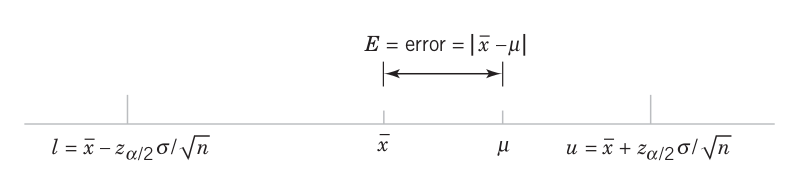
interval_sample_size.png

\[\left( \overline{X} - 2.58 \dfrac{\sigma}{\sqrt{n}}, \overline{X} + 2.58 \dfrac{\sigma}{\sqrt{n}} \right)\]

The interval length is \[5.16 \dfrac{\sigma}{\sqrt{n}}\]

\[n = (51.6 \sigma)^2 = 51.6 \approx 52\]

If \(\overline{x}\) is used as an estimate of \(\mu\), we can be \(100(1-a)%\) confident that the error \(|\overline{x}-\mu|\) will not exceed \(E\) when the sample size is \[n=\left( \dfrac{z_{a/2}\sigma}{E} \right)^2\]

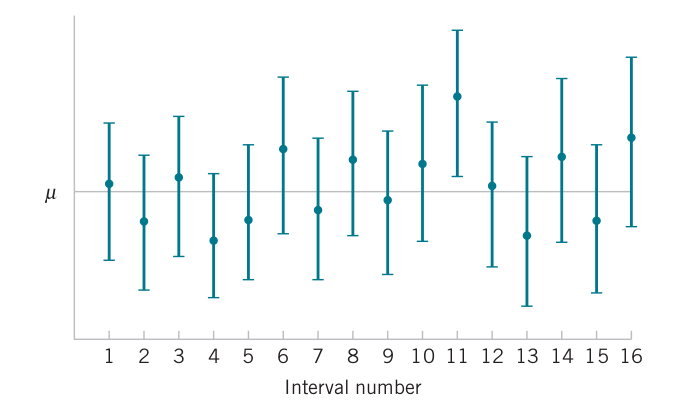
Interpreting a confidence interval

  • Probability of \(\mu\) being within the CI we calculated?
  • Subtle difference between probability and confidence
  • The CI is itself a random interval
ci_interpretation.png

Problem 17.4

The average speed of vehicles on a highway is being studied. Observations on 50 vehicles yielded a mean of 65 mph. Assume that the standard deviation is known to be 6 mph. What is the 2-sided 99% confidence interval on the mean speed?

How many additional vehicles need to be observed so that the mean speed can be estimated within \(\pm 1\) mph with 99% confidence?

If two engineers collect data and each one separately observes 10 vehicles, what is the probability that Engineer 1 will have a sample mean larger than Engineer's 2 by 2 mph?

What if the two engineers observed 100 vehicles instead?