Probability & Statistics in Engineering
Fall 2023 - 12 Sep
Random experiments
- Repeat measurements of current in copper wire
- What are some factors that can cause variations in measurements?
- Ambient temperature
- Small impurities in the wire
- Current source drifts
- Random component in the experiment
Random experiment
An experiment that can result in different outcomes, even though it is repeated in the same manner every time
Noise variables affect transformation of inputs to outputs
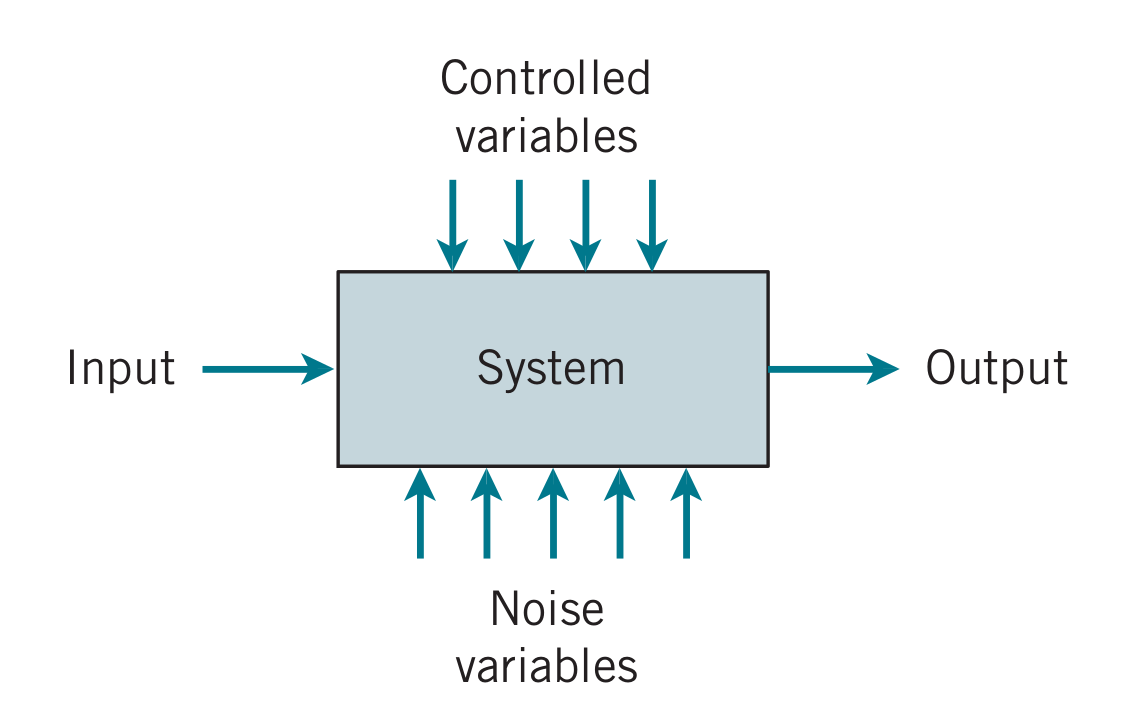
Example
A contractor needs to acquire bulldozers for a new project and from prior experience knows that there is a 50% chance that each bulldozer will remain operational for at least 6 months. If they purchased 3 bulldozers, what is the probability that there will be only 1 bulldozer that is operational after 6 months?
Sample space
The set of all possible outcomes of a random experiment is called the sample space of the experiment, denoted as \(S\)
depends on the objective
Consider measurements of the recycle time of a flash for a camera, what is the sample space for:
- Recycle time
- If recycle times are between 1.5 and 5 secs
- If objective is whether time is low, medium or high
- If objective is whether camera meets a specification threshold
- $S$={x > 0}
- $S$={1.5 < x < 5>}
- $S$={low, medium, high}
- $S$={yes, no}
Discrete vs continuous sample spaces
- When sample points are discrete entities and countable: discrete space
- When sample space consists of a continuum of sample points: continuous space
- Locations of possible traffic accidents on a bridge?
- Number of flaws in a given length of welding?
- Bearing capacity of clay soil deposit that is between 1.5 and 4.0 tons/ft2?
Events
An event is a subset of the sample space of a random experiment
Example
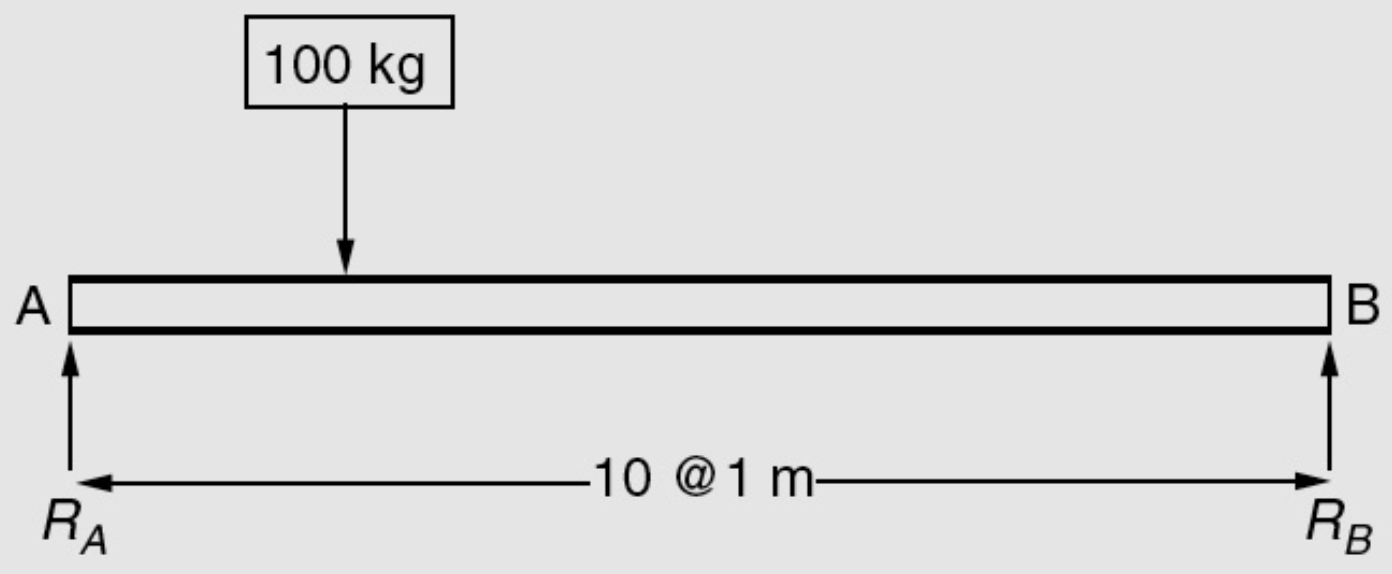
- What is the sample space for the reaction \(R_A\)?
- What is the probability of the event \(10 \leq R_A \leq 20\,\mathrm{kg}\)?
- What is the probability of the event \(R_A \geq 60\,\mathrm{kg}\)?
Combination of events
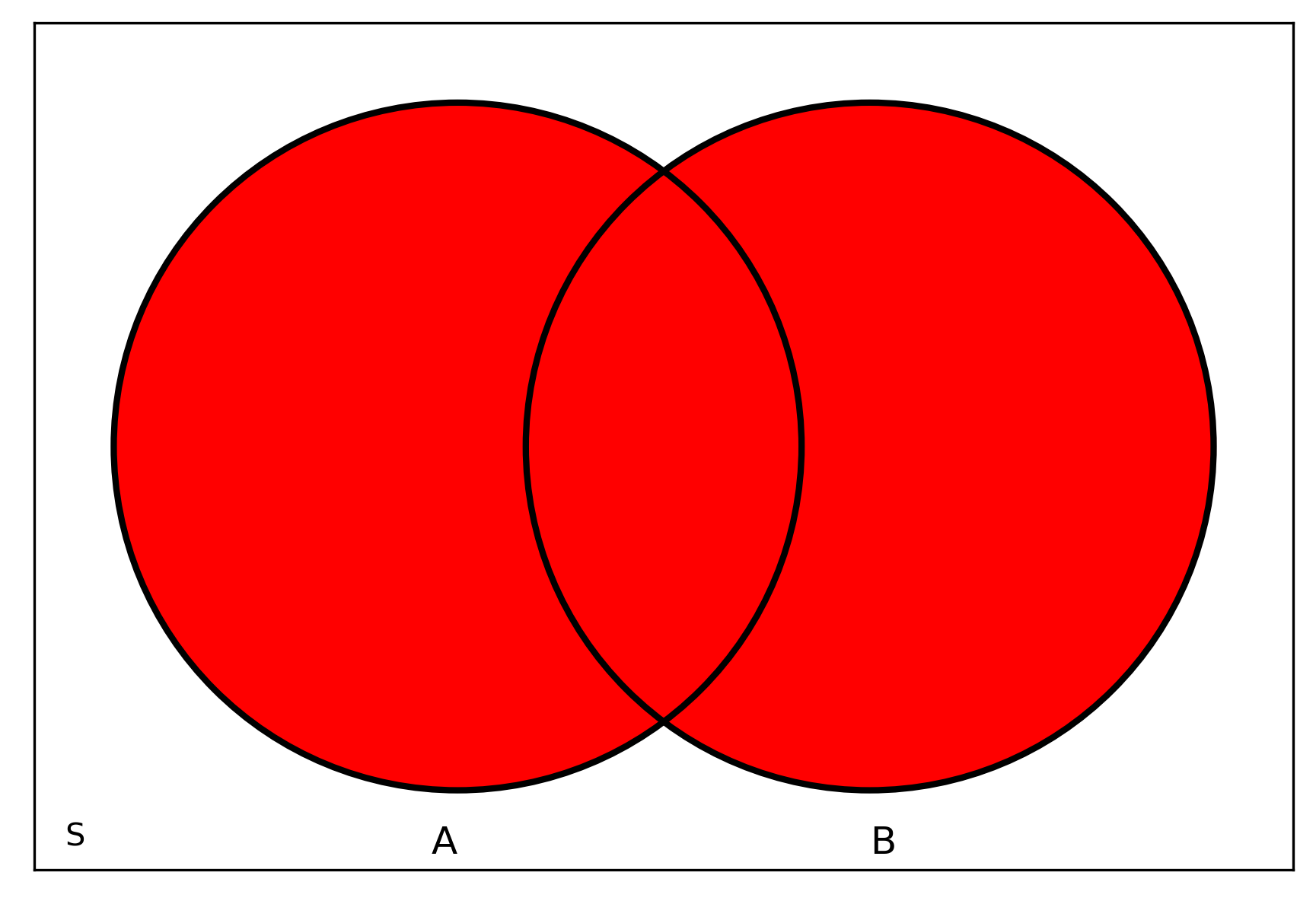
- union of two events is the event that consists of all outcomes contained in either of two events
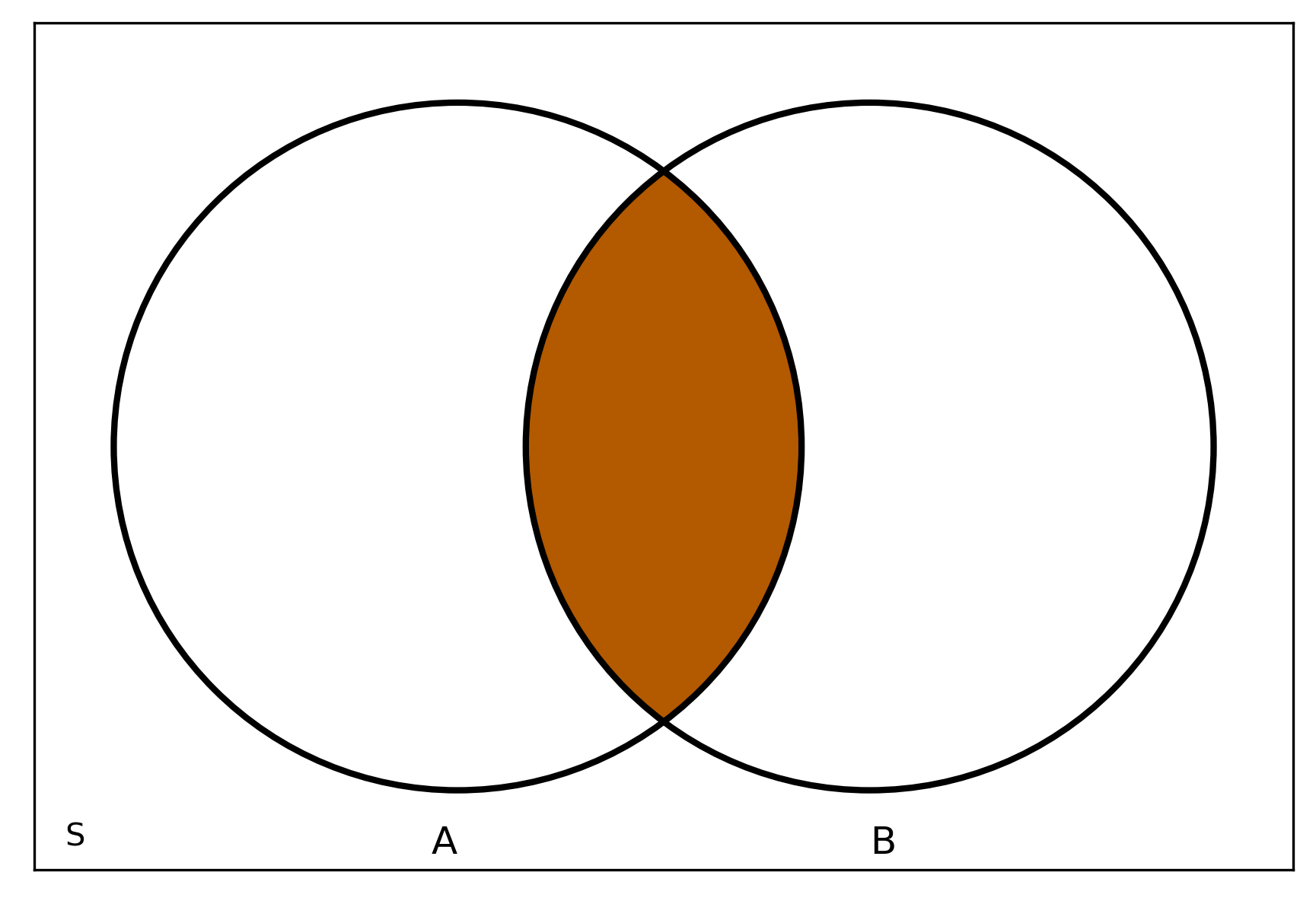
- intersection of two events is the event that consists of all outcomes contained in both events
- complement of an event is the set of outcomes that are not in the event
Venn diagrams
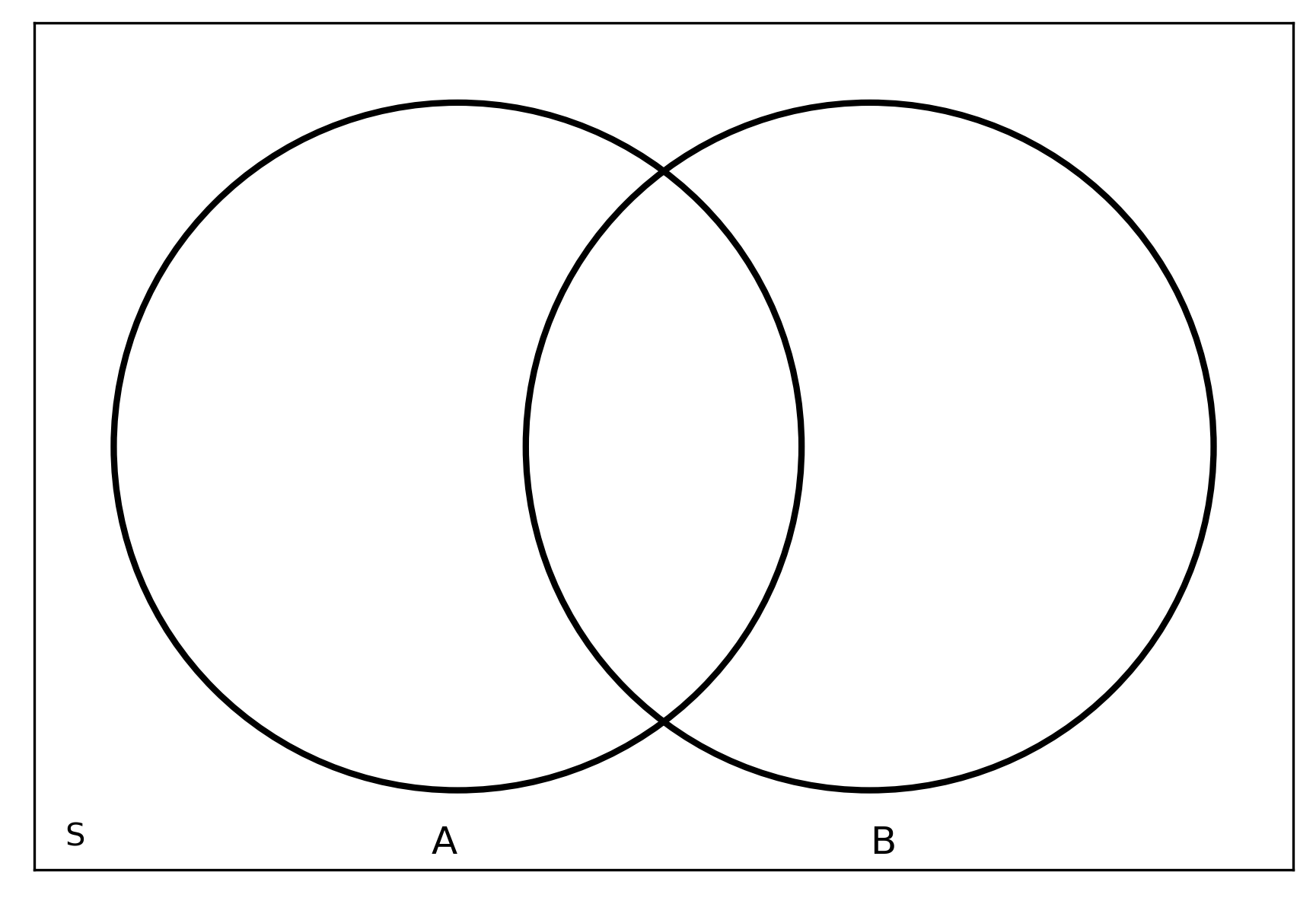
Event \(A\)
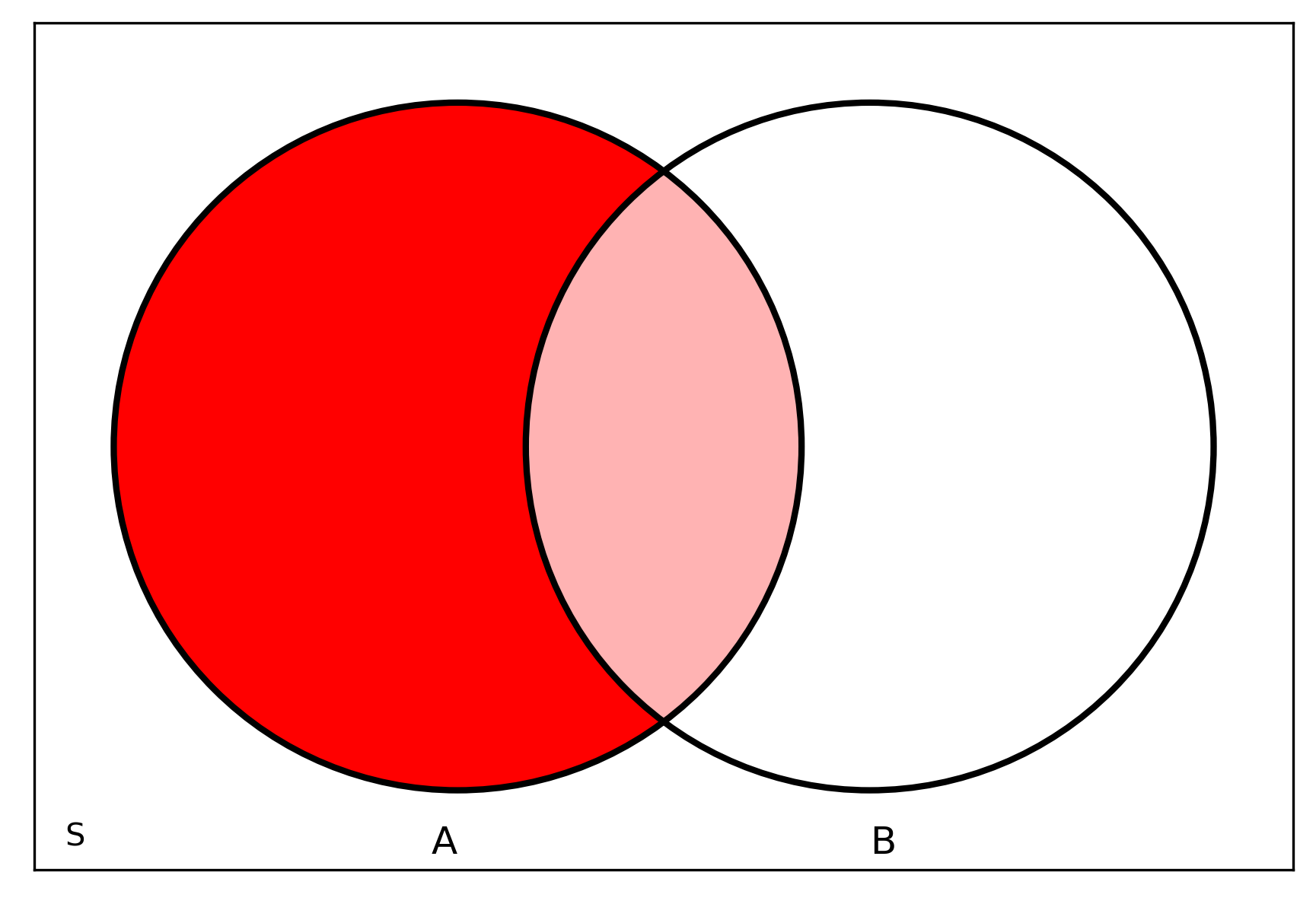
Union \(A \cup B\)
Intersection \(A \cap B\)
Complement \(A^c\)
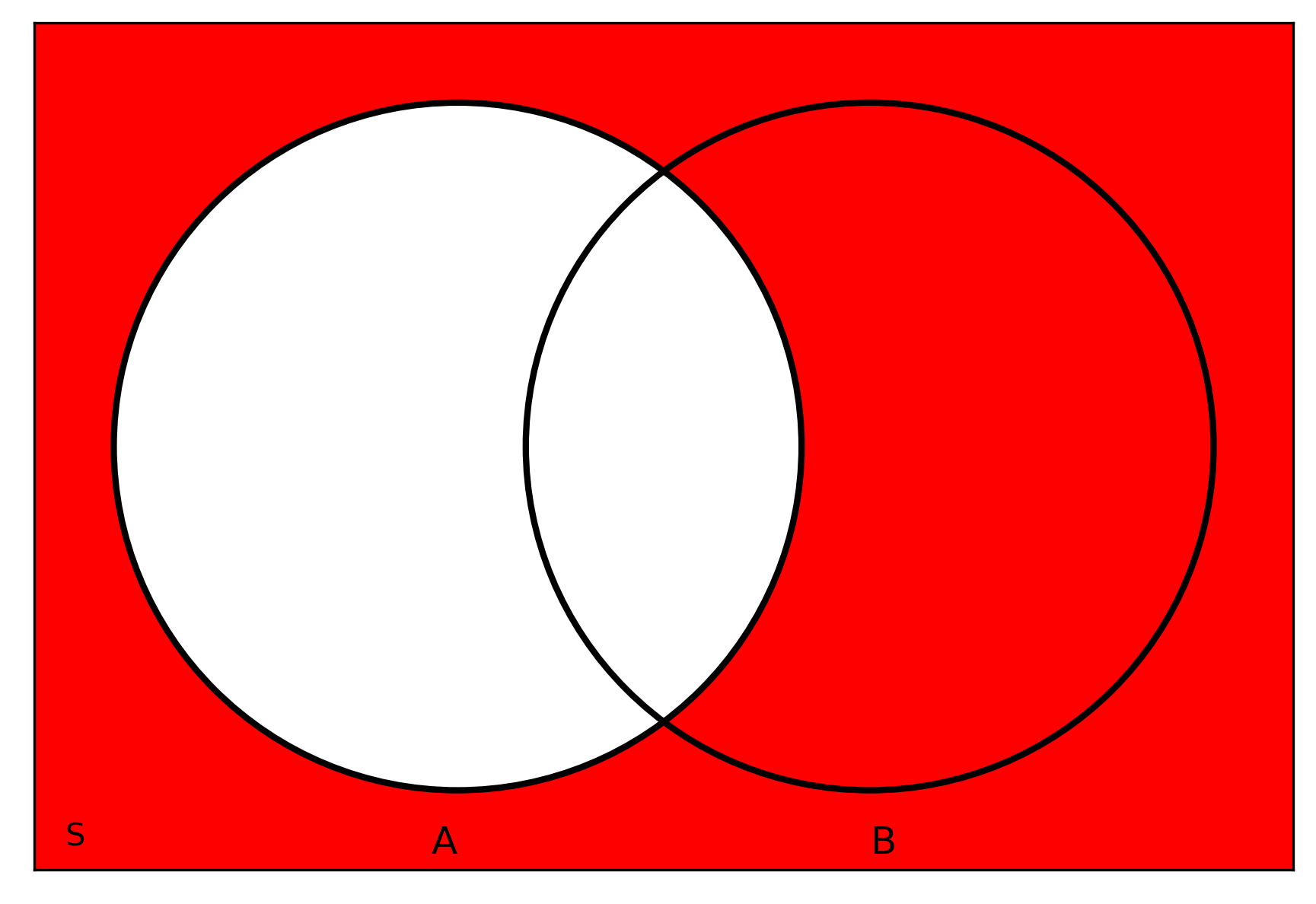
Complement \((AB)^c\)
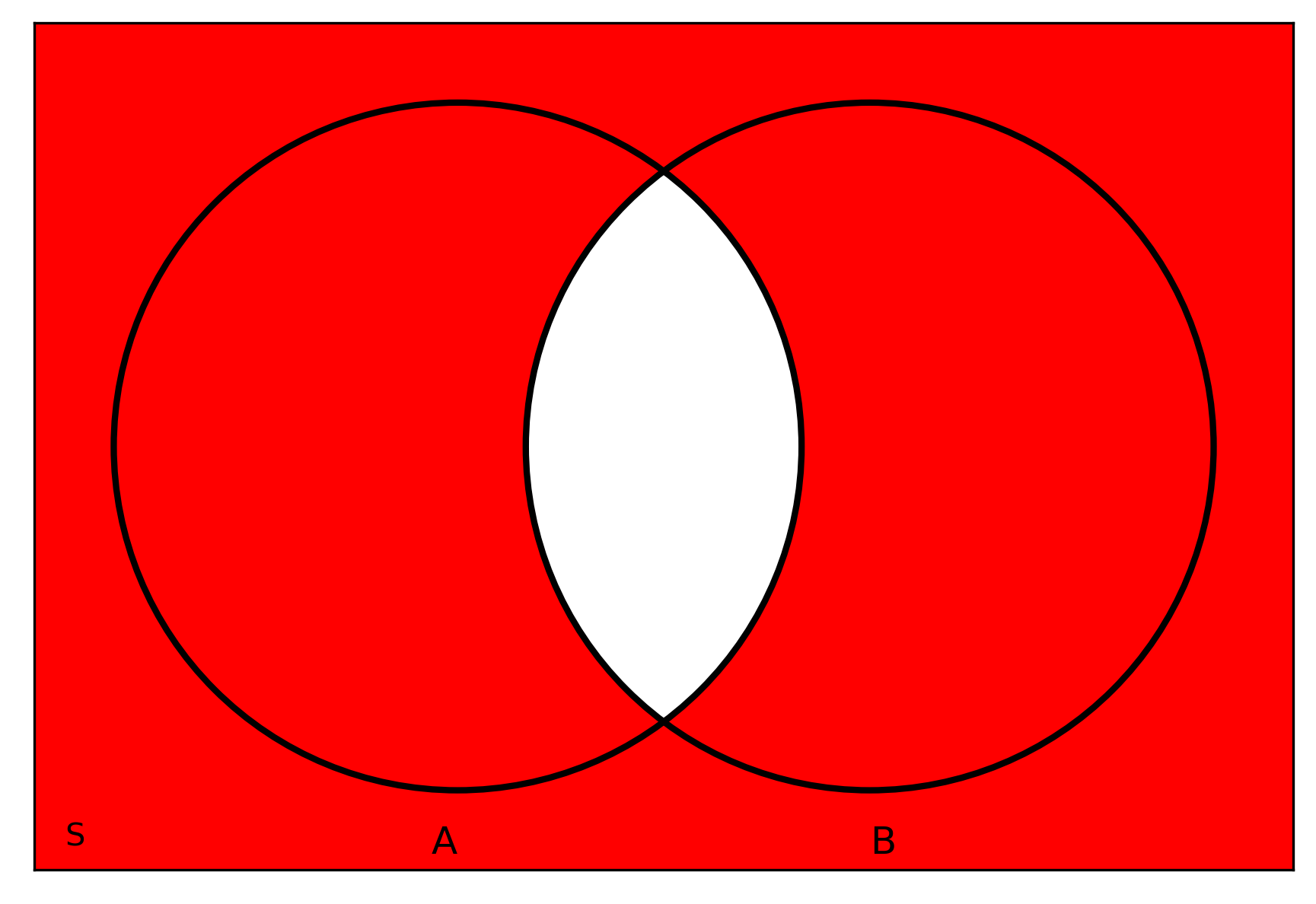
Complement relations
\[(A^c)^c = A\]
\[A \cup A^c = S\]
Contained events \(A \subset B\)
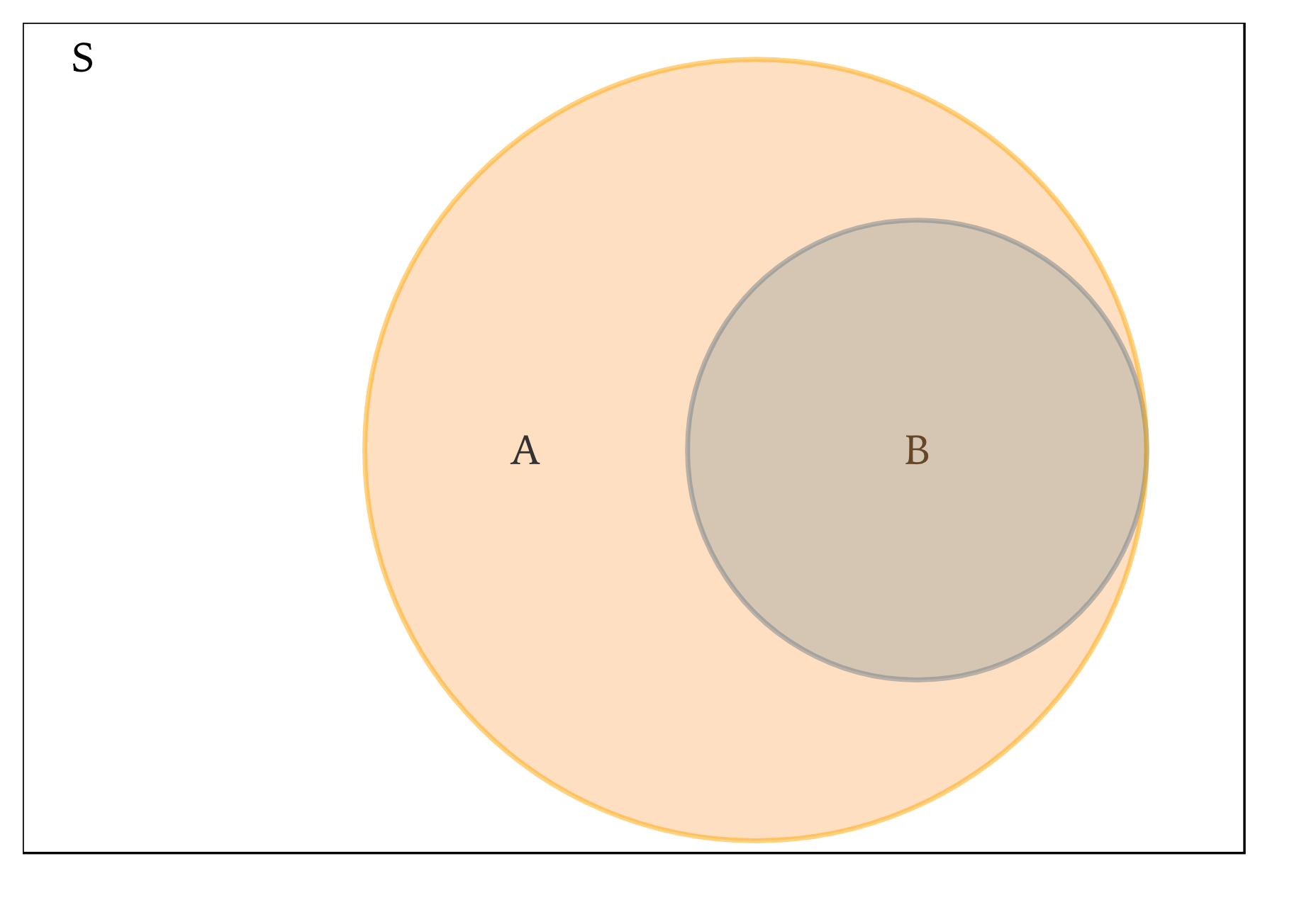
Mutually exclusive events
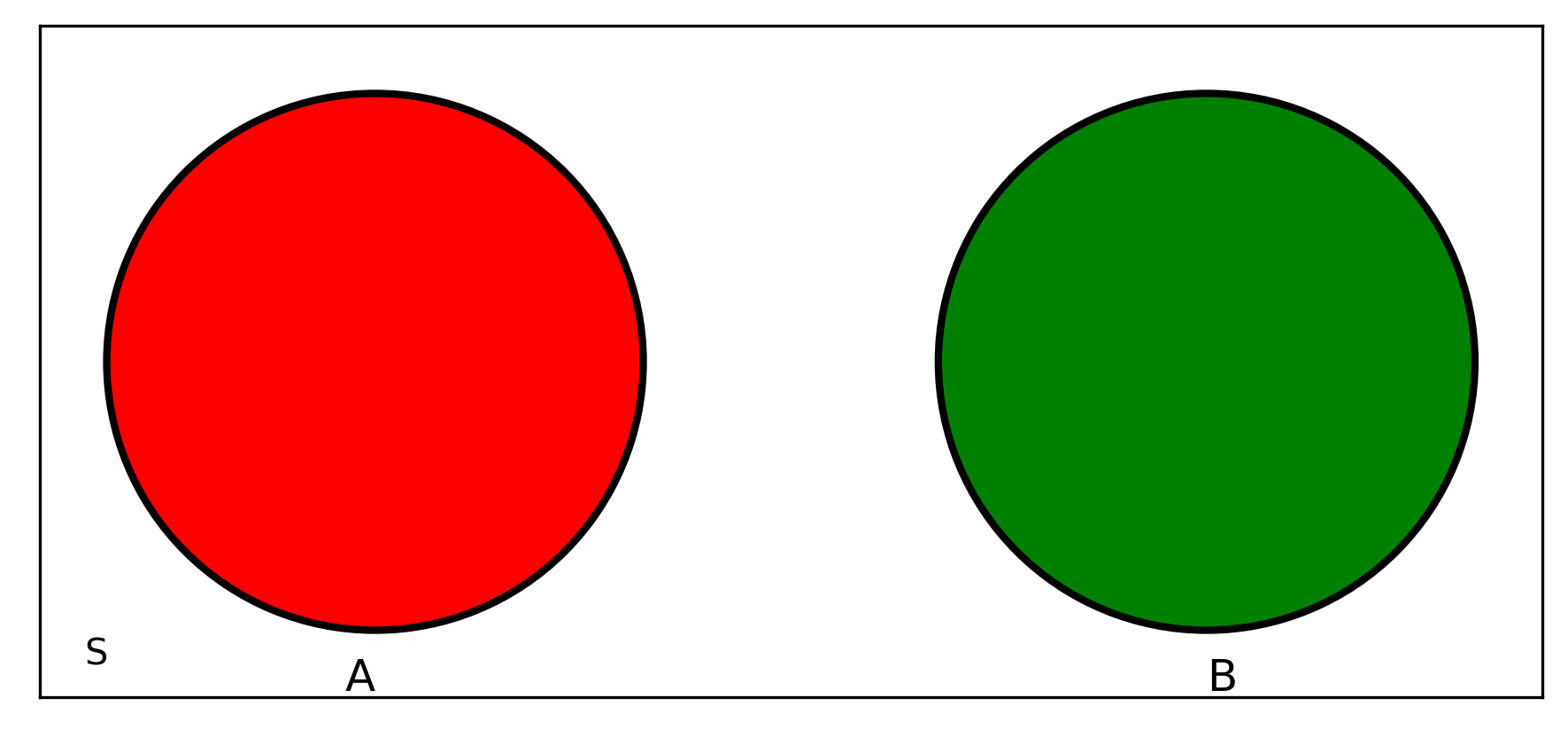
Empty set
Mutually exclusive intersection \[ A \cap B = \emptyset \]
\[ A \cap A^c = \emptyset \]
\[S^c = \emptyset \]
Let's recap
Hands-on exercise
Let \(A\), \(B\), and \(C\) are three events. Find expressions for the following events:
- only \(A\) occurs
- both \(A\) and \(C\) occur but not \(B\) occurs
- at least one of the events occurs
- all three occur
- none of the events occur
- at most one of them occurs
- exactly two of them occur
Mathematical operations
\[A \cup A = A\] \[A \cap A = A\]
\[A \cup S = S\] \[A \cap S = A\]
Commutative rule
\[A \cup B = B \cup A\] \[A \cap B = B \cap A\]
Associative rule
\[(A \cup B) \cup C = A \cup (B \cup C)\] \[(A \cap B) \cap C = A \cap (B \cap C)\]
Distributive rule
\[(A \cup B) \cap C\]
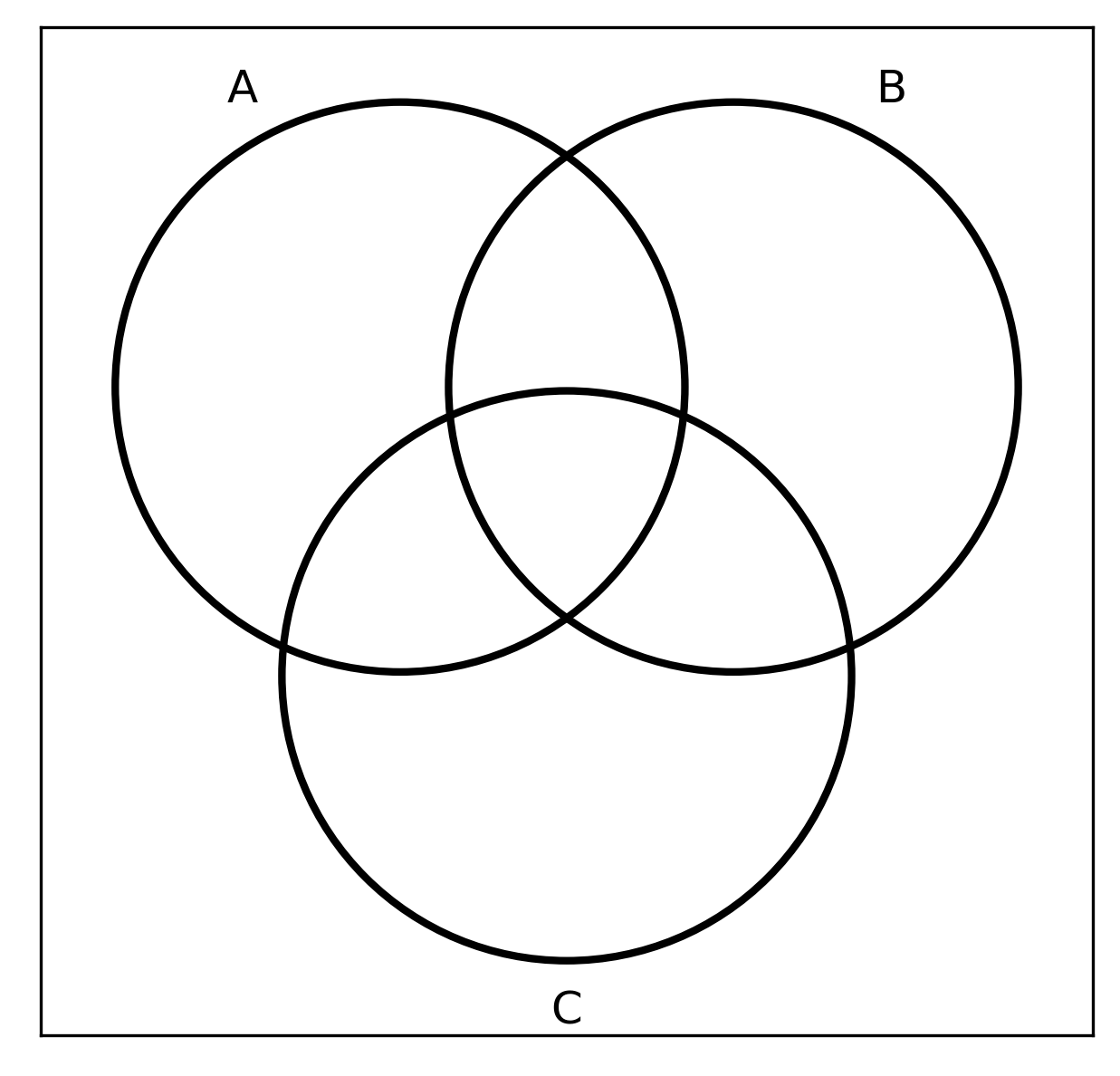
\[(A \cap C) \cup (B \cap C)\]

Distributive rule
\[(A \cup B) \cap C = (A \cap C) \cup (B \cap C)\] \[(A \cap B) \cup C = (A \cup C) \cap (B \cup C)\]
DeMorgan's law
For two sets (or events) \(A\) and \(B\)
\[(A \cup B)^c = A^c \cap B^c\]
\[(A \cup B)^c\]

\[A^C \cap B^c\]

General DeMorgan's law
\[(E_1 \cup E_2 \cup ... \cup E_n)^c = E_1^c \cap E_2^c \cap ... \cap E_n^c\]
\[(E_1^c \cup E_2^c \cup ... \cup E_n^c)^c = E_1 \cap E_2 \cap ... \cap E_n\]
\[(E_1 \cap E_2 \cap ... \cap E_n)^c = E_1^c \cup E_2^c \cup ... \cup E_n^c\]
Problem 1
The direction of wind at a site is between due East (\(\theta=0^{\mathrm{\circ}}\)) and due North (\(\theta=90^{\mathrm{\circ}}\)). The wind speed \(V\) can be any positive value.
- Sketch the sample space for wind speed and direction.
- Denote the events \[E_1=(V > 35 \,\mathrm{kph})\] \[E_2=(15\,\mathrm{kph} < V \leq 45\,\mathrm{kph})\] \[E_3 = (\theta \leq 30^{\mathrm{\circ}})\] Identify the events \(E_1\), \(E_2\), \(E_3\), and \(E_1^c\).
- Identify the events \(A=E_1 \cap E_3\), \(B=E_1 \cup E_2\), and \(C=E_1 \cap E_2 \cap E_3\). Are events \(A\) and \(B\) mutually exclusive? How about events \(A\) and \(C\)?
Problem 2
Consider a simple chain that would fail if either link breaks: \(E_1\) breakage of link 1 and \(E_2\) breakage of link 2.

Define the failure of the chain and non-failure in terms of \(E_1\) and \(E_2\).
Problem 3
Water supply for two cities C and D comes from sources A and B via pipelines 1-4.
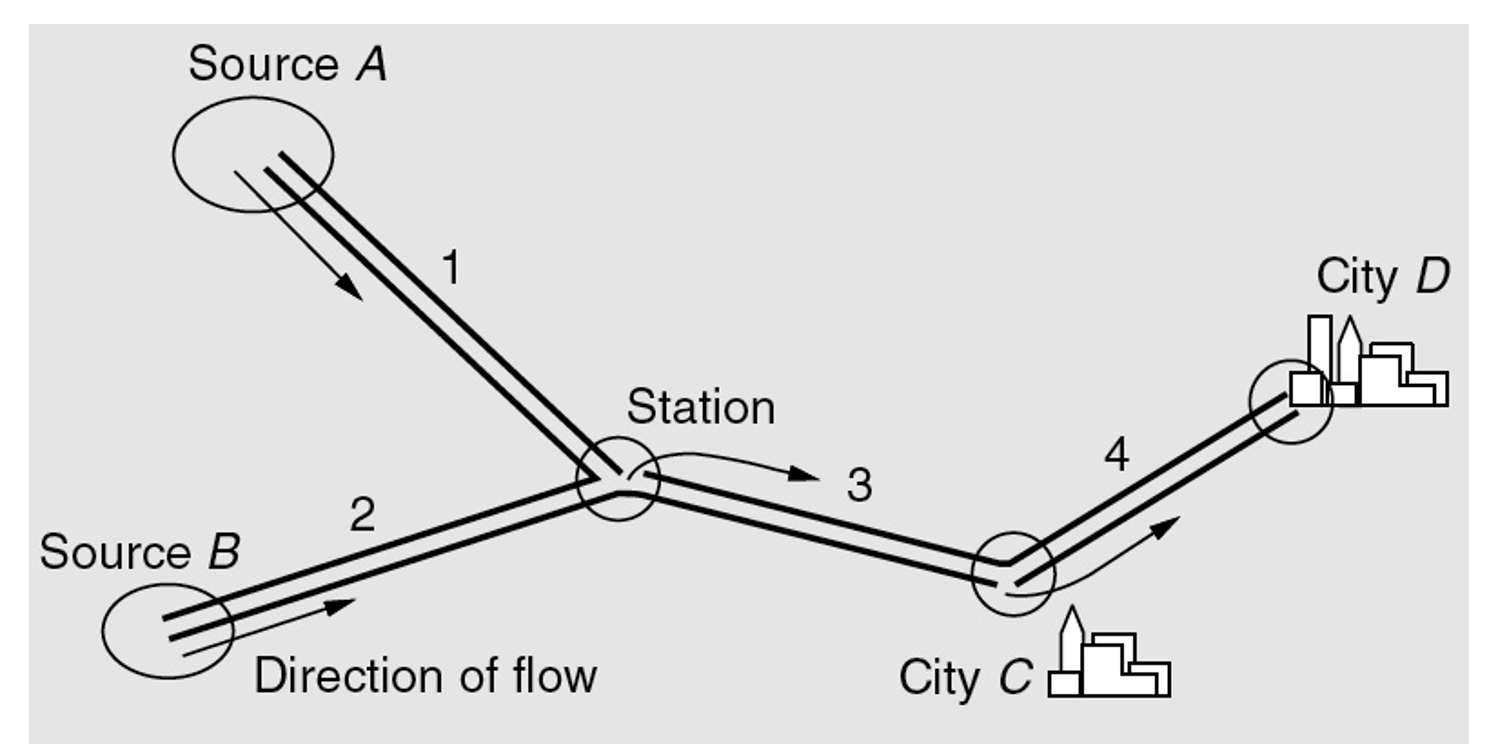 Assume that either one of the sources is by itself sufficient to supply water to both cities. If \(E_i\) is the failure of branch \(i\), describe the events of no shortage in each of the cities.
Assume that either one of the sources is by itself sufficient to supply water to both cities. If \(E_i\) is the failure of branch \(i\), describe the events of no shortage in each of the cities.