Probability & Statistics in Engineering

Fall 2022 - 6 Sep

Introductions

Logistics

  • Office hours: Thu 10am-1pm
  • TuTh 1-2:15pm
  • Echo360 lecture recordings
  • Supplemental Instruction: Julia Leventis

Grading

   
Homework 30%
Midterm 30%
Final 35%
Quizzes 5%

Textbook

textbook.jpg



D. Montgomery & G. Runger, Applied Probability and Statistics for Engineers, Wiley

and some additional notes on specific topics (e.g., Bayes' theorem)

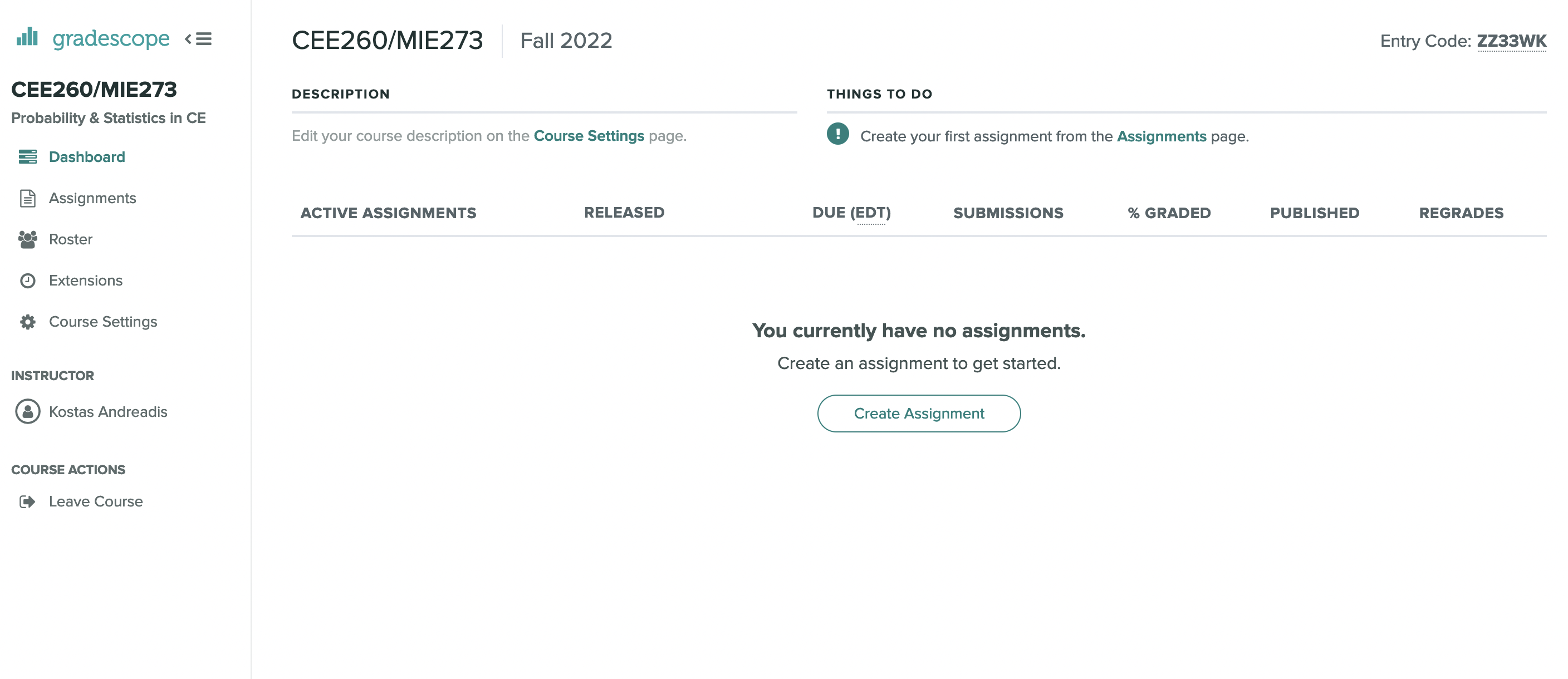
Gradescope

gradescope.png https://www.gradescope.com/courses/427843

  • Disability Statement

http://www.umass.edu/disability/

  • Inclusivity

https://engineering.umass.edu/about-us/inclusivity-statement

  • Academic Honesty Policy Statement

http://umass.edu/dean_students/codeofconduct/acadhonesty/

Course objvectives

  • Understand the fundamental concepts of probability (e.g., independence, expectation, density functions)
  • Identify, apply and evaluate the proper probability model for different systems
  • Utilize statistical methods to make inferences about systems from data
  • Perform regression analyses, test hypotheses, and calculate confidence intervals for solving engineering problems
  • Acquire a basic understanding of statistical inference and sampling theory

Schedule

Week 1 Statistics in engineering
Week 2 Probability concepts
Week 3 Discrete variables
Week 4 Continuous variables
Week 5 Probability distributions
Week 6 Joint probability
Week 7 Conditional probability
Week 8 Central limit theorem; Midterm
Week 9 Point estimation
Week 10 Confidence intervals
Week 11 Hypothesis testing
Week 12 NO CLASS
Week 13 Inference for two samples
Week 14 Linear regression

news.png

People can come up with statistics to prove anything. Forty percent of all people know that

homer.jpg

Engineering method

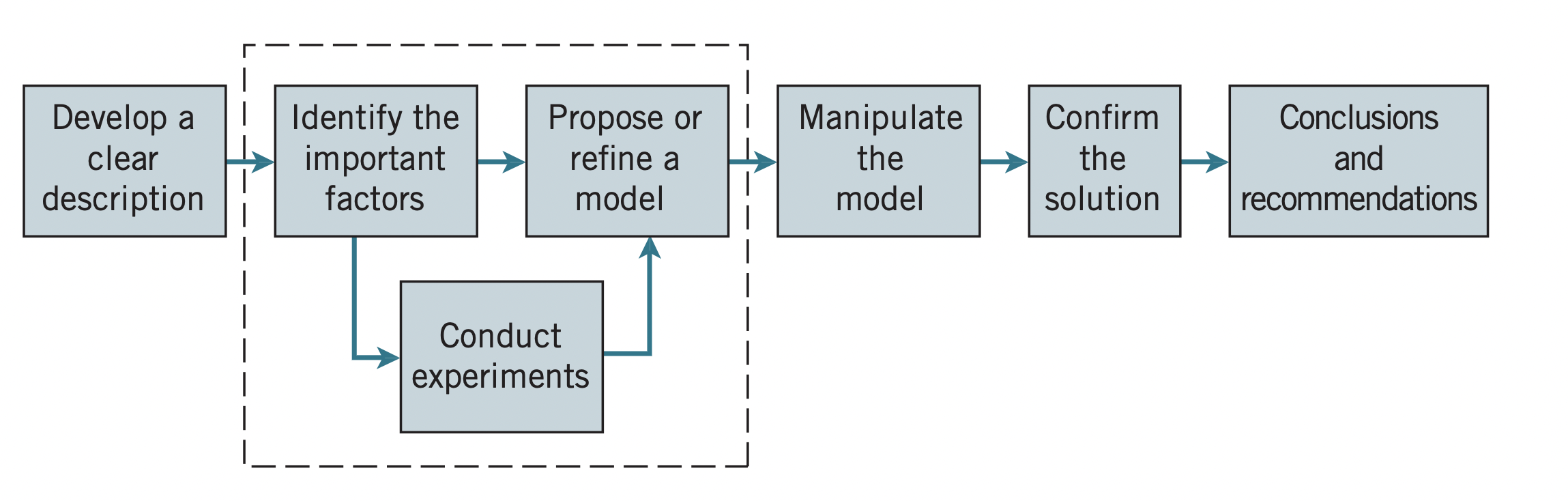
engineering_method.png

What about uncertainty?

Uncertainty

  • Randomness with the underlying process that is exhibited as variability
  • Aleatory uncertainty
  • Inherent in nature and cannot be reduced
  • Imperfect or insufficient models of the process of interest
  • Epistemic uncertainty
  • Improved models or measurements could reduce it

Aleatory uncertainty

Variability - Randomness

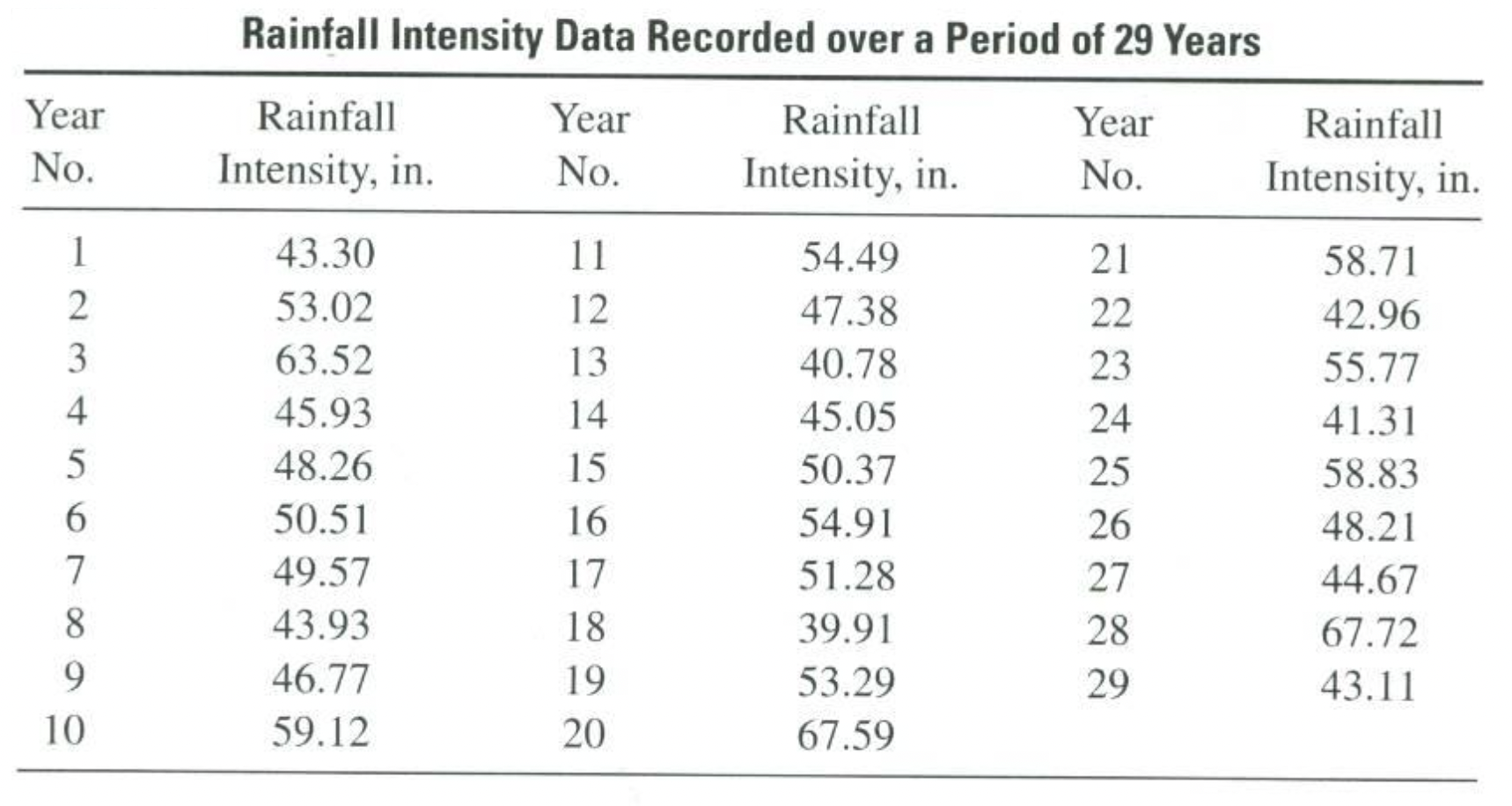
rainfall_table.png

Histograms

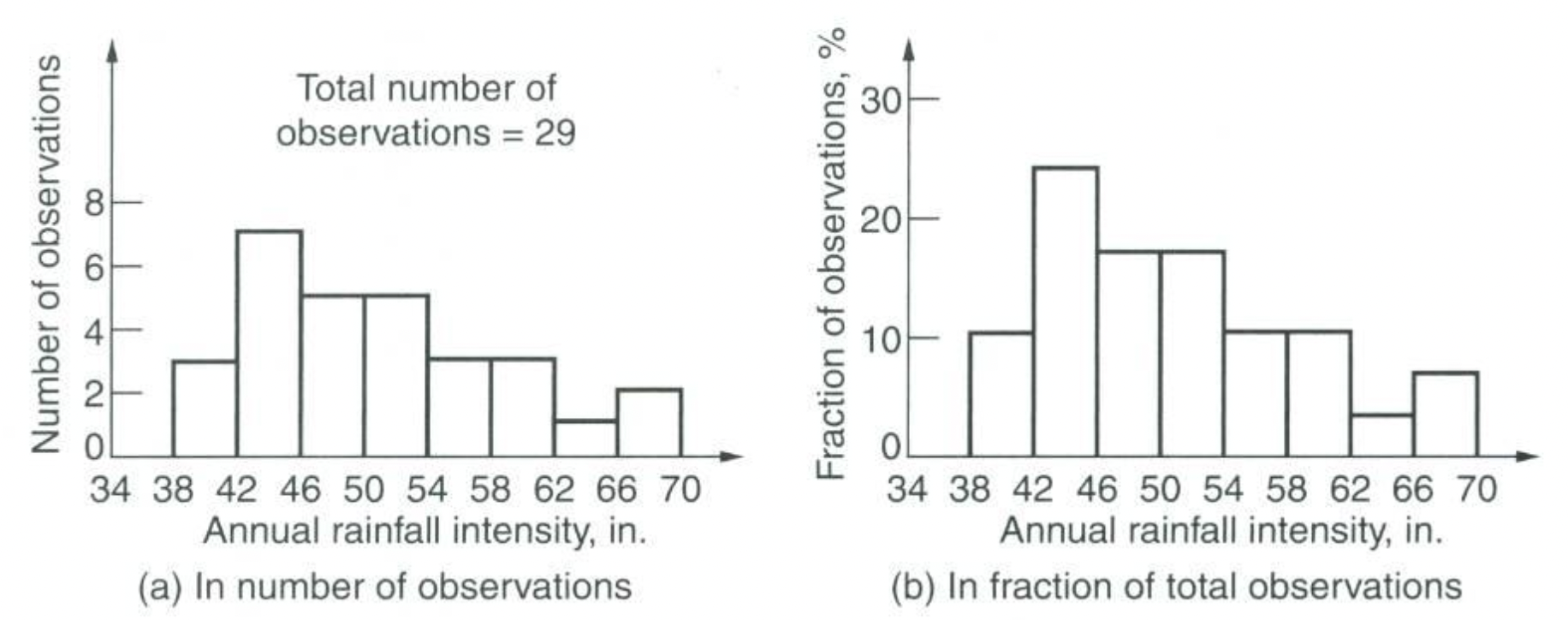
rainfall_histograms.png

Joint variability

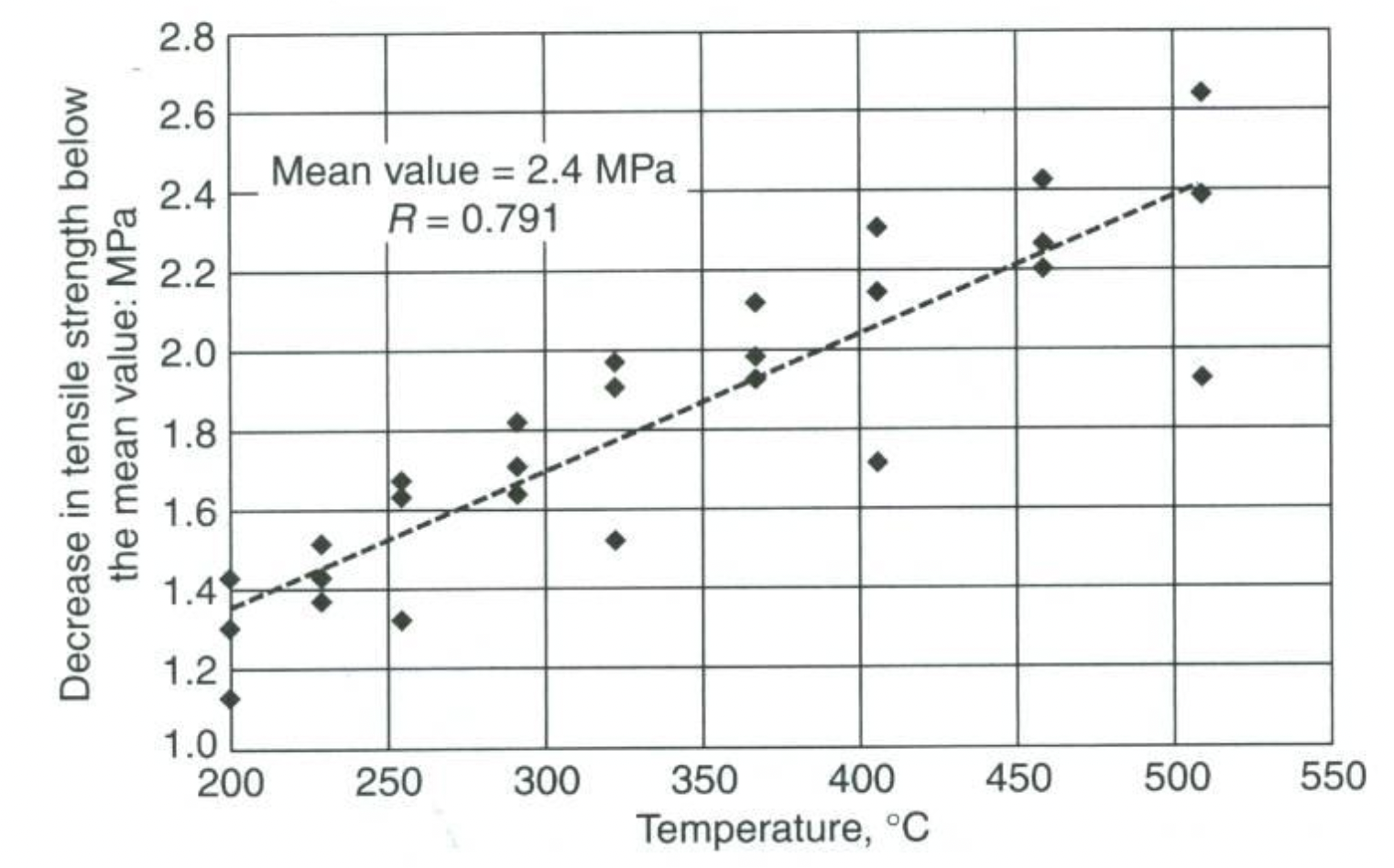
dos_santos.png

Epistemic uncertainty

  • Predictions and analysis require models
  • All models are wrong, but some are useful
  • Reducible uncertainty as more knowledge is gained

Example

cantilever_beam.png

\[ \Delta_B = \dfrac{P L^3}{3 E I}\]

  • Material is linearly elastic
  • Beam remains plane under load \(P\)
  • Support of the beam at point \(A\) is perfectly rigid

Decision making under uncertainty

  • No single observation is representative of the system
  • Evaluation or predictions are based on imperfect models
  • Statistics allow us to describe the unavoidable uncertainty
  • Make decisions based on trade offs (cost, benefit etc.)

Population and samples

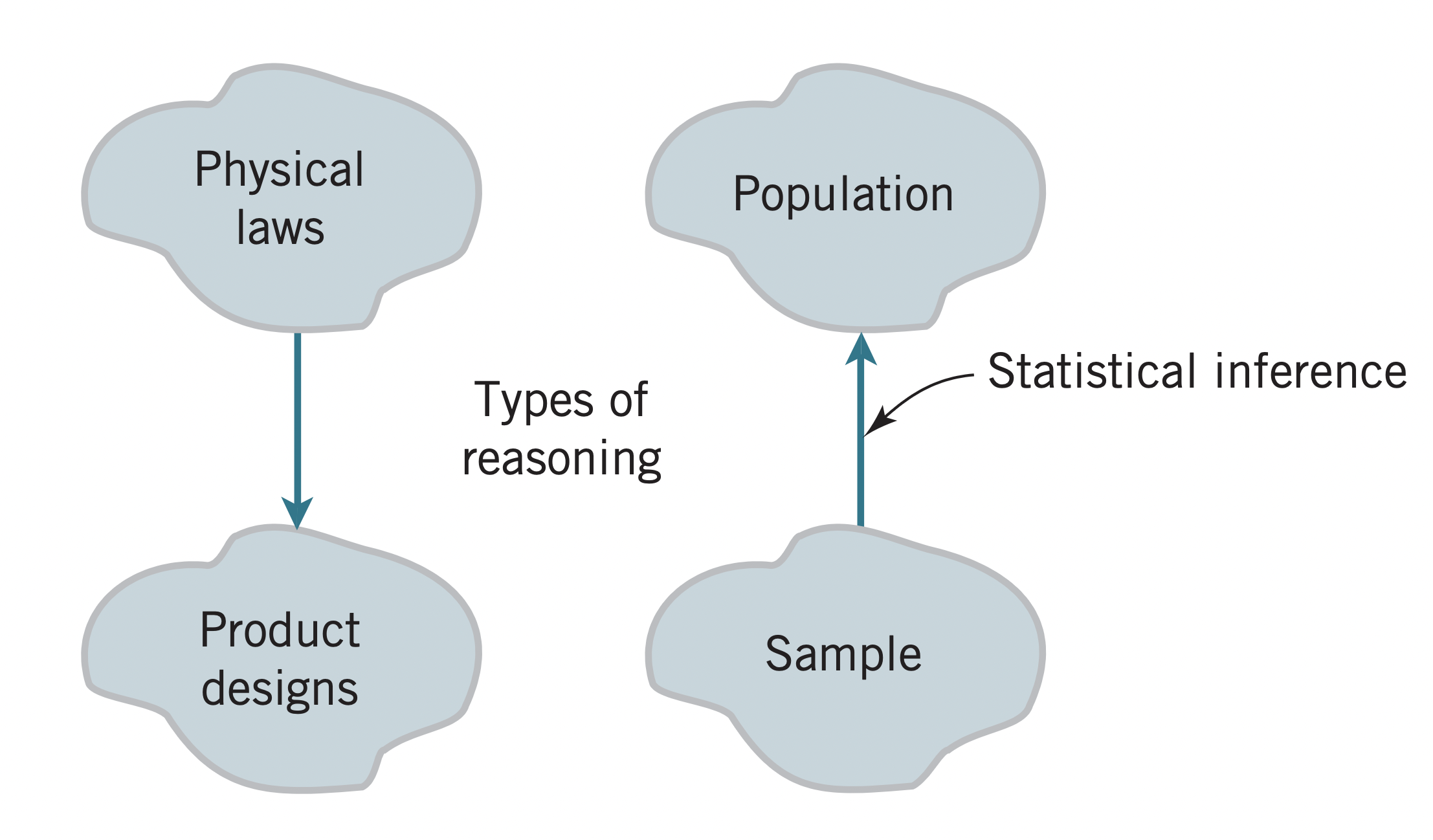
statistical_inference.png

  • Mechanistic models
  • Empirical models
  • Statistical inference
  • Probability models

Readings

  • Section 1.1
  • Section 1.2.1
  • Sections 1.3-1.4